Digital Electronics
This topic is an extension of the topic of Boolean Algebra which includes a more thorough description of the category in terms of determining whether a circuit results in a TRUE or FALSE value using truth tables or how to simplify a circuit to as few gates as possible. Electrical engineers use the following symbols to design electrical circuits that are used inside the computer’s hardware. The following table illustrates the equivalent Boolean algebra expression and truth table for each gate.
Definitions
Sample Problems
Sample Problem 1
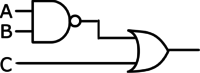
Find all ordered triplets (A, B, C) which make the following circuit FALSE:
Solution:
One approach to solving this problem is to reason about that inputs and outputs are necessary at each gate. For the circuit to be FALSE, both inputs to the file OR gate must be false. Thus, input C must be FALSE, and the output of the NAND gate must also be false. The NAND gate is false only when both of its inputs are TRUE; thus, inputs A and B must both be TRUE. The final answer is (TRUE, TRUE, FALSE), or (1, 1, 0).
Another approach to solving this problem is to translate the circuit into a Boolean Algebra expression and simplify the expression using the laws of Boolean Algebra. This circuit translates to the Boolean expression [math]\overline{AB}+C[/math]. To find when this is FALSE we can equivalently find when the [math]\overline{\overline{AB}+C}[/math] is TRUE. The expression becomes [math]\overline{\overline{AB}}\cdot C[/math] after applying DeMorgan’s Law. The double NOT over the AB expression cancels out, to become [math]AB\overline{C}[/math]. The AND of 3 terms is TRUE when each term is TRUE, or A=1, B=1 and C=0.
Sample Problem 2
Find all ordered 4-tuples (A, B, C, D), which make the following circuit TRUE:
Solution:
We'll use a truth table to solve this problem. The rows in the truth table will correspond to all possible inputs - 16 in this case, since there are 4 inputs. The output columns will be the output of each gate, other than the NOT gates.
[math]A[/math] [math]B[/math] [math]C[/math] [math]D[/math] [math]1[/math] [math]2[/math] [math]3[/math] [math]4[/math] [math]5[/math] 0 0 0 0 1 1 0 1 0 0 0 0 1 0 1 0 1 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 1 1 0 1 0 0 1 1 1 0 1 0 1 0 1 0 0 1 1 1 0 1 1 0 0 1 1 1 1 0 1 1 1 0 0 1 1 1 1 0 0 0 1 1 0 1 0 1 0 0 1 0 1 0 1 1 1 0 1 0 0 1 0 1 1 1 0 1 1 0 1 0 1 1 1 1 0 0 1 1 0 1 0 1 1 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0
This circuit diagram translates to: [math](\overline{C+D}+B) \oplus (\overline{A}B) \oplus (\overline{C+D})[/math]. The table has the following headings: 1=[math]\overline{C+D}[/math], 2=[math]1+\overline{B}[/math], 3=[math]\overline{A}B[/math], 4=[math]A \oplus B[/math], and 5=[math]4 \oplus 1[/math]. Thus, the 4-tuples (0,0,0,0), (1,0,0,0), (1,1,0,0), (1,1,0,1), (1,1,1,0), and (1,1,1,1) all make the circuit FALSE.
Video Resources
The following YouTube videos show ACSL students and advisors working out some ACSL problems that have appeared in previous contests. Some of the videos contain ads; ACSL is not responsible for the ads and does not receive compensation in any form for those ads.
https://youtu.be/z9s8A8oBe7g Logic Gate Expressions Kevin Drummhttps://youtu.be/TLl4E3IV6Z0 Logic Gate Combinations Kevin Drumm