Karnaugh Maps
Introduction
Logic design implies the analysis, synthesis, minimization, and implementation of binary functions.
Combinational logic refers to networks whose output is strictly dependent on the inputs. The analysis of such networks requires first the writing of the Boolean algebraic equation representative of the network, and then the complete characterization of the output as a result of all the possible combinations of the inputs.
Minimization involves reducing the Boolean algebraic expression to some minimal form.
Any minimization tool in Boolean is based on the algebraic theorems. Algebraic reduction of Boolean functions is not easy and requires considerable experience, judgement and luck. It becomes more apparent as the complexity of the function increases. As a result extensive effort has been devoted toward developing techniques, aids or tools, that will allow the logic designer to minimize a function. The Venn diagram, Veitch diagram, Karnaugh map, Quine-McCluskey method, and other techniques have all been developed with but one objective-to allow the designed to arrive at a minimal expression as rapidly as possible with the least amount of effort.
Amoung these methods the Karnaugh Maps (made by G. Karnaugh in 1953) will be presented bellow.
The Karnaugh map technique is thought to be the most valuable tool available for dealing with Boolean functions. It provides instant recognition of the basic patterns, can be used to obtain all possible combinations and minimal terms, and is easily applied to all varieties of complex problems. Minimization with the map is accomplished through recognition of basic patterns.
The appearance of 1’s in adjacent cells immediately identifies the presence of a redundant variable.
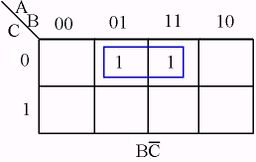
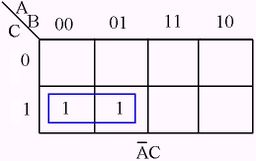
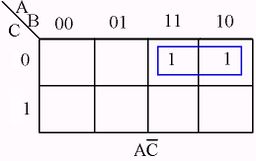
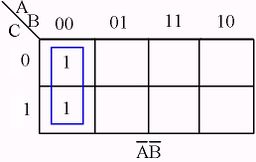
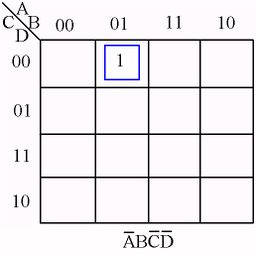
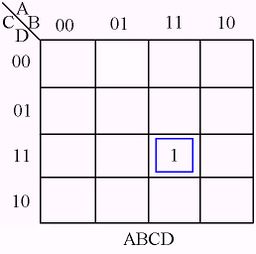
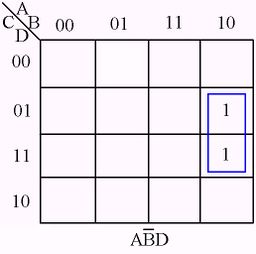
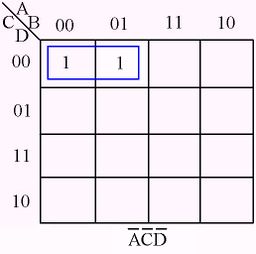
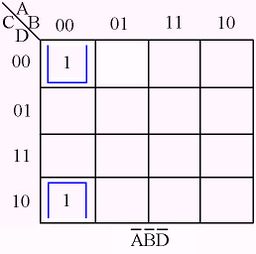
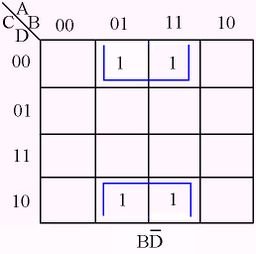
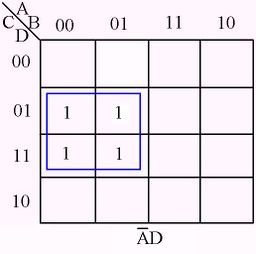
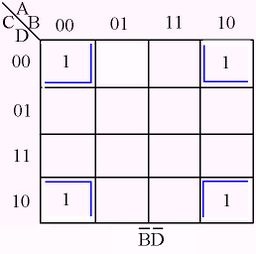
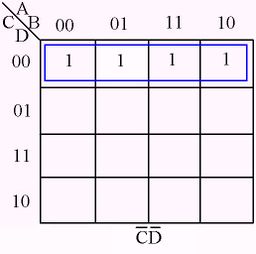
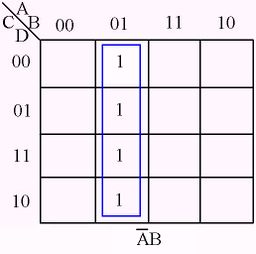
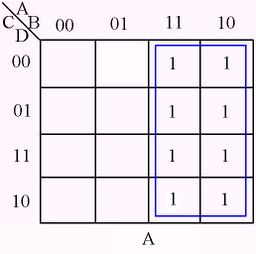
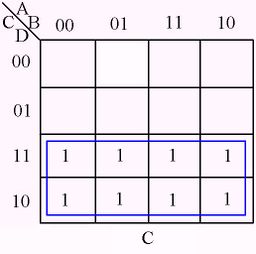
The following figures illustrate some examples of minimizing with a three-variable map and four-variable map.[1]
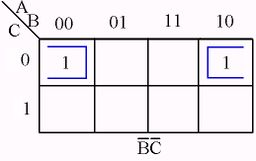
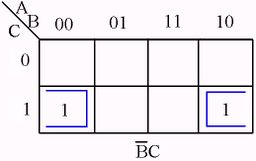
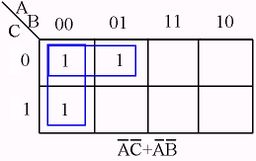
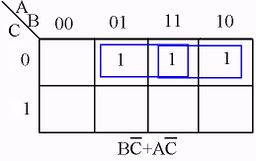
Karnaugh Map examples
RULES SUMMARY
No zeros allowed.
No diagonals.
Only power of 2 number of cells in each group.
Groups should be as large as possible.
Every one must be in at least one group.
Overlapping allowed.
Wrap around allowed.
Fewest number of groups possible.
Sample problems
Sample problem 1
Karnaugh Map to minimize a digital circuit
| Initial circuit | Karnaugh Map | AND/OR circuit |
|---|---|---|
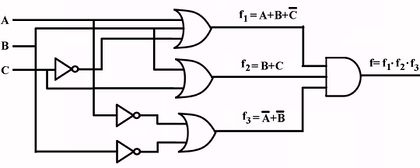 |
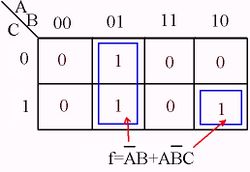 |
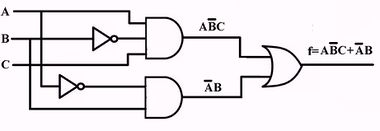
|
1. William E. Wickes, Logic Design with Integrated Circuits, John Willey & Sons, Inc, New York-London-Sydney