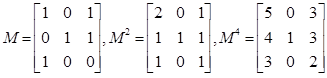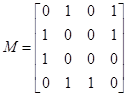Difference between revisions of "Graph Theory"
Marc Brown (talk | contribs) |
Marc Brown (talk | contribs) |
||
| Line 6: | Line 6: | ||
::[[File:Graph fig1a.svg|150px]] <span style="display:inline-block; width: 5em;"></span>[[File:Graph fig1b.svg|150px]] | ::[[File:Graph fig1a.svg|150px]] <span style="display:inline-block; width: 5em;"></span>[[File:Graph fig1b.svg|150px]] | ||
The precise way to represent this graph is to identify its set of vertices {A, B, C, D, E, F, G}, and its set of edges between these vertices {AB, AD, BD, CF, FG, GH, GE, HE}. | |||
To be precise, the graph above is an ''undirected graph''; the edge from x to y is the same as from y to x. | |||
== Terminology == | == Terminology == | ||
A ''path'' from vertex x to y in a graph is a list of vertices, in which successive vertices are connected by edges in the graph. For example, FGHE is path from F to E in the graph above. A ''simple path'' is a path with no vertex repeated. For example, FGHEG is not a simple path. | |||
A path from vertex | A graph is ''connected'' if there is a path from every vertex to every other vertex in the graph. Intuitively, if the vertices were physical objects and the edges were strings connecting them, a connected graph would stay in one piece if picked up by any vertex. A graph which is not connected is made up of ''connected components''. For example, the graph above has two connected components: {A, B,D} and {C, E, F, G, H}. | ||
A | A ''cycle'' is a path, which is simple except that the first and last vertex are the same (a path from a point back to itself). For example, the path HEGH is a cycle in our example. Vertices must be listed in the order that they are traveled to make the path; any of the vertices may be listed first. Thus, HEGH and EHGE are different ways to identify the same cycle. For clarity, we list the start / end vertex twice: once at the start of the cycle and once at the end. | ||
We’ll denote the number of vertices in a given graph by V, the number of edges by E. Note that E can range anywhere from V to V2 (or 1/2 V(V-1) in an undirected graph). Graphs will all edges present are called ''complete graphs''; graphs with relatively few edges present (say less than V log(V)) are called ''sparse''; graphs with relatively few edges missing are called ''dense.'' | |||
== Trees == | |||
A graph with no cycles is called a ''tree''. There is only one path between any two nodes in a tree. A tree on N vertices contains exactly N-1 edges. A ''spanning tree'' of a graph is a subgraph that contains all the vertices and forms a tree. A group of disconnected trees is called a ''forest.'' | |||
== Directed Graphs == | |||
Directed graphs are graphs which have a direction associated with each edge. An edge xy in a directed graph can be used in a path that goes from x to y but not necessarily from y to x. For example, a directed graph similar to our example graph is drawn below: | ''Directed graphs'' are graphs which have a direction associated with each edge. An edge xy in a directed graph can be used in a path that goes from x to y but not necessarily from y to x. For example, a directed graph similar to our example graph is drawn below: | ||
[[File:graph_4.png]] | [[File:graph_4.png]] | ||
| Line 31: | Line 35: | ||
== Adjacency Matrices == | == Adjacency Matrices == | ||
It is frequently convenient to represent a graph by a matrix, as shown in the second sample problem below. If we consider vertex A as 1, B as 2, etc., then a “one” in M at row i and column j indicates that there is | It is frequently convenient to represent a graph by a matrix, as shown in the second sample problem below. If we consider vertex A as 1, B as 2, etc., then a “one” in M at row i and column j indicates that there is an edge from vertex i to j., whereas a "zero" indicates there is not an edge. If we raise M to the pth power, the resulting matrix indicates which paths of length p exist in the graph. The value | ||
in $M^p(i,j)$ is the number of paths from vertex i to vertex j. | in $M^p(i,j)$ is the number of paths from vertex i to vertex j. | ||
== Sample Problems == | == Sample Problems == | ||
=== | === Problem 1 === | ||
Find the number of different cycles contained in the directed graph with vertices {A, B, C, D, E} and edges {AB, BA, BC, CD, DC, DB, DE}. | Find the number of different cycles contained in the directed graph with vertices {A, B, C, D, E} and edges {AB, BA, BC, CD, DC, DB, DE}. | ||
| Line 66: | Line 70: | ||
--> | --> | ||
=== | === Problem 2=== | ||
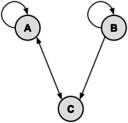
In the following directed graph, find the total number of different paths from vertex A to vertex C of length 2 or 4. | In the following directed graph, find the total number of different paths from vertex A to vertex C of length 2 or 4. | ||
| Line 80: | Line 84: | ||
There is 1 path of length 2 (M 2[1,3]) and 3 paths of length 4 (M 4[1,3]). | There is 1 path of length 2 (M 2[1,3]) and 3 paths of length 4 (M 4[1,3]). | ||
=== | === Problem 3 === | ||
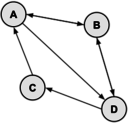
Given the adjacency matrix, draw the directed graph. | Given the adjacency matrix, draw the directed graph. | ||
Revision as of 00:13, 6 September 2018
Many problems are naturally formulated in terms of points and connections between them. For example, a computer network has PCs connected by cables, an airline map has cities connected by routes, and a school has rooms connected by hallways. A graph is a mathematical object which models such situations.
Overview
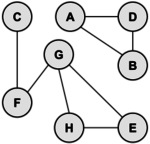
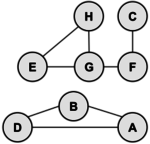
A graph is a collection of vertices and edges. An edge is a connection between two vertices (sometimes referred to as nodes). One can draw a graph by marking points for the vertices and drawing lines connecting them for the edges, but the graph is defined independently of the visualrepresentation. For example, the following two drawings represent the same graph:
The precise way to represent this graph is to identify its set of vertices {A, B, C, D, E, F, G}, and its set of edges between these vertices {AB, AD, BD, CF, FG, GH, GE, HE}.
To be precise, the graph above is an undirected graph; the edge from x to y is the same as from y to x.
Terminology
A path from vertex x to y in a graph is a list of vertices, in which successive vertices are connected by edges in the graph. For example, FGHE is path from F to E in the graph above. A simple path is a path with no vertex repeated. For example, FGHEG is not a simple path.
A graph is connected if there is a path from every vertex to every other vertex in the graph. Intuitively, if the vertices were physical objects and the edges were strings connecting them, a connected graph would stay in one piece if picked up by any vertex. A graph which is not connected is made up of connected components. For example, the graph above has two connected components: {A, B,D} and {C, E, F, G, H}.
A cycle is a path, which is simple except that the first and last vertex are the same (a path from a point back to itself). For example, the path HEGH is a cycle in our example. Vertices must be listed in the order that they are traveled to make the path; any of the vertices may be listed first. Thus, HEGH and EHGE are different ways to identify the same cycle. For clarity, we list the start / end vertex twice: once at the start of the cycle and once at the end.
We’ll denote the number of vertices in a given graph by V, the number of edges by E. Note that E can range anywhere from V to V2 (or 1/2 V(V-1) in an undirected graph). Graphs will all edges present are called complete graphs; graphs with relatively few edges present (say less than V log(V)) are called sparse; graphs with relatively few edges missing are called dense.
Trees
A graph with no cycles is called a tree. There is only one path between any two nodes in a tree. A tree on N vertices contains exactly N-1 edges. A spanning tree of a graph is a subgraph that contains all the vertices and forms a tree. A group of disconnected trees is called a forest.
Directed Graphs
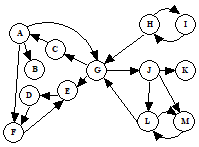
Directed graphs are graphs which have a direction associated with each edge. An edge xy in a directed graph can be used in a path that goes from x to y but not necessarily from y to x. For example, a directed graph similar to our example graph is drawn below:
There is only one directed path from D to F. Note that there are two edges between H and I, one each direction, which essentially makes an undirected edge. An undirected graph can be thought of as a directed graph with all edges occurring in pairs in this way. A dag (directed acyclic graph) is a directed graph with no cycles.
Adjacency Matrices
It is frequently convenient to represent a graph by a matrix, as shown in the second sample problem below. If we consider vertex A as 1, B as 2, etc., then a “one” in M at row i and column j indicates that there is an edge from vertex i to j., whereas a "zero" indicates there is not an edge. If we raise M to the pth power, the resulting matrix indicates which paths of length p exist in the graph. The value in $M^p(i,j)$ is the number of paths from vertex i to vertex j.
Sample Problems
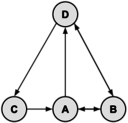
Problem 1
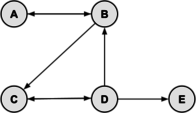
Find the number of different cycles contained in the directed graph with vertices {A, B, C, D, E} and edges {AB, BA, BC, CD, DC, DB, DE}.
Solution: The graph is as follows:
By inspection, the cycles are: {A,B}, {B,C,D} and {C,D}. Thus, there are 3 cycles in the graph.
Problem 2
In the following directed graph, find the total number of different paths from vertex A to vertex C of length 2 or 4.
Solution:
Let matrix M represent the graph. Recall that the number of paths from vertex i to vertex j of length p equals M p[i,j]. The values of M, M 2 and M 4 are:
There is 1 path of length 2 (M 2[1,3]) and 3 paths of length 4 (M 4[1,3]).
Problem 3
Given the adjacency matrix, draw the directed graph.
Solution:
The vertices do not have to be in those exact locations, but the edges must be the same. In particular, there must be exactly 7 edges: AB, AD, BA, BD, CA, DB, and DC. Here are two valid drawings of the graph:
Video Resources
ACSL Videos
The following YouTube videos show ACSL students and advisors working out some ACSL problems that have appeared in previous contests. Some of the videos contain ads; ACSL is not responsible for the ads and does not receive compensation in any form for those ads.
| ACSL - Graph Theory Worksheet 1 (misterminich)
Shows the solution to the ACSL problem: 'Draw the directed graph with vertices A, B, C, D, E and the directed edges AB, BC, AD, BC, DC, ED, and EA. | |
| ACSL Graph Theory Worksheet 3 (misterminich)
Shows the solution to an ACSL problem asking to find how many paths of a specific length there are in a specific directed graph. | |
| Graph Theory ACSL Example Problem (Tangerine Code)
Shows the solution to an ACSL problem asking to find how many different cycles there are from a specific vertex in a specific directed graph. |
Other Videos
There are many dozens of YouTube videos that cover introductions to graph theory. The following are a couple that we found particularly nicely done. Be aware thqt the videos contain ads; ACSL is not responsible for the ads and does not receive compensation in any form for those ads.
| CS 106B Lecture: Graphs: basic concepts
This lecture from Stanford University is s wonderful introduction to graph theory. The lecture starts out with many examples of real world problems that are modeled by graphs, and then moves on to review basic terminology relating to graph theory. | |
| Data structures: Introduction to Graphs (mycodeschool)
A nice introduction to the fundamental concepts of graphs. |