Difference between revisions of "FSAs and Regular Expressions"
| Line 185: | Line 185: | ||
|- | |- | ||
| ()|| '''Groups.''' | | ()|| '''Groups.''' | ||
Regular expressions allow us to not just match text but also to '''extract information for further processing. | Regular expressions allow us to not just match text but also to '''extract information | ||
for further processing. | |||
This is done by defining '''groups of characthers''' and capturing them using | This is done by defining '''groups of characthers''' and capturing them using | ||
the parentheses '''()'''. | the parentheses '''()'''. | ||
| Line 193: | Line 194: | ||
|- | |- | ||
| \number || '''Backreference.''' | | \number || '''Backreference.''' | ||
A set of different symbols of a regular expression can be grouped together to act as a single unit and behave as a block. | A set of different symbols of a regular expression can be grouped together to act as a single unit | ||
and behave as a block. | |||
'''\n''' means that the group enclosed within the '''n-th''' bracket will be repeated at current position. | '''\n''' means that the group enclosed within the '''n-th''' bracket will be repeated at current position. | ||
Revision as of 03:28, 14 August 2020
A Finite State Automaton (FSA) is a mathematical model of computation comprising all 4 of the following: 1) a finite number of states, of which exactly one is active at any given time; 2) transition rules to change the active state; 3) an initial state; and 4) one or more final states. We can draw an FSA by representing each state as a circle, the final state as a double circle, the start state as the only state with an incoming arrow, and the transition rules as labeled-edges connecting the states. When labels are assigned to states, they appear inside the circle representing the state.
In this category, FSAs will be limited to parsing strings. That is, determining if a string is valid or not.
Basics
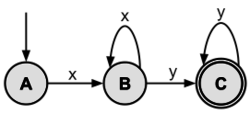
Here is a drawing of an FSA that is used to parse strings consisting of x's and y's:
In the above FSA, there are three states: A, B, and C. The initial state is A; the final state is C. The only way to go from state A to B is by seeing the letter x. Once in state B, there are two transition rules: seeing the letter y will cause the FSA to make C the active state, and seeing an x will keep B as the active state. State C is a final state so if the string being parsed is completed and the FSA is in State C, the input string is said to be accepted by the FSA. In State C, seeing any additional letter y will keep the machine in state C. The FSA above will accept strings composed of one or more x’s followed by one or more y’s (e.g., xy, xxy, xxxyy, xyyy, xxyyyy).
A Regular Expression (RE) is an algebraic representation of an FSA. For example, the regular expression corresponding to the first FSA given above is xx*yy*.
The rules for forming a Regular Expression (RE) are as follows:
- 1. The null string (λ) is a RE.
- 2. If the string a is in the input alphabet, then it is a RE.
- 3. if a and b are both REs, then so are the strings built up using the following rules:
- a. CONCATENATION. "ab" (a followed by b).
- b. UNION. "aUb" or "a|b" (a or b).
- c. CLOSURE. "a*" (a repeated zero or more times). This is known as the Kleene Star.
The order of precedence for Regular Expression operators is: Kleene Star, concatenation, and then union. Similar to standard Algebra, parentheses can be used to group sub-expressions. For example, "dca*b" generates strings dcb, dcab, dcaab, and so on, whereas "d(ca)*b" generates strings db, dcab, dcacab, dcacacab, and so on.
If we have a Regular Expression, then we can mechanically build an FSA to accept the strings which are generated by the Regular Expression. Conversely, if we have an FSA, we can mechanically develop a Regular Expression which will describe the strings which can be parsed by the FSA. For a given FSA or Regular Expression, there are many others which are equivalent to it. A "most simplified" Regular Expression or FSA is not always well defined.
Regular Expression Identities
| 1. (a*)* = a* |
| 2. aa* = a*a |
| 3. aa* U λ = a* |
| 4. a(b U c) = ab U ac |
| 5. a(ba)* = (ab)*a |
| 6. (a U b)* = (a* U b*)* |
| 7. (a U b)* = (a*b*)* |
| 8. (a U b)* = a*(ba*)* |
RegEx in Practice
Programmers use Regular Expressions (usually referred to as regex) extensively for expressing patterns to search for. All modern programming languages have regular expression libraries.
Unfortunately, the specific syntax rules vary depending on the specific implementation, programming language, or library in use. Interactive websites for testing regexes are a useful resource for learning regexes by experimentation. An excellent online tool is https://regex101.com/. A very nice exposition is Pattern Matching with Regular Expressions from the Automate the Boring Stuff book and online course.
Here are the additional syntax rules that we will use. They are pretty universal across all regex packages.
| Pattern | Description |
|---|---|
| | | As described above, a vertical bar separates alternatives. For example, gray|grey can match "gray" or "grey". |
| * | As described above, the asterisk indicates zero or more occurrences of the preceding element. For example, ab*c matches "ac", "abc", "abbc", "abbbc", and so on. |
| ? | The question mark indicates zero or one occurrences of the preceding element. For example, colou?r matches both "color" and "colour". |
| + | The plus sign indicates one or more occurrences of the preceding element. For example, ab+c matches "abc", "abbc", "abbbc", and so on, but not "ac". |
| . | The wildcard . matches any character. For example, a.b matches any string that contains an "a", then any other character, and then a "b" such as "a7b", "a&b", or "arb", but not "abbb". Therefore, a.*b matches any string that contains an "a" and a "b" with 0 or more characters in between. This includes "ab", "acb", or "a123456789b". |
| [ ] | A bracket expression matches a single character that is contained within the brackets. For example, [abc] matches "a", "b", or "c". [a-z] specifies a range which matches any lowercase letter from "a" to "z". These forms can be mixed: [abcx-z] matches "a", "b", "c", "x", "y", or "z", as does [a-cx-z]. |
| [^ ] | Matches a single character that is not contained within the brackets. For example, [^abc] matches any character other than "a", "b", or "c". [^a-z] matches any single character that is not a lowercase letter from "a" to "z". Likewise, literal characters and ranges can be mixed. |
| ( ) |
As described above, parentheses define a sub-expression. For example, the pattern H(ä|ae?)ndel matches "Handel", "Händel", and "Haendel". |
More useful patterns
| Pattern | Description | REGEX | Sample match | Sample
not match |
|---|---|---|---|---|
| \d | Digit.
Matches any digit. Equivalent with [0-9]. |
\d\d\d | 123 | 1-3 |
| \D | Non digit.
Matches any character that is not a digit. |
\d\D\d | 1-3 | 123 |
| \w | Word.
Matches any alphanumeric character and underscore. Equivalent with [a-zA-Z0-9_]. |
\w\w\w | a_A | a-A |
| \W | Not Word.
Matches any character that is not word character (alphanumeric character and underscore). |
\W\W\W | +-$ | +_@ |
| \s | Whitespace.
Matches any whitespace character (space, tab, line breaks). |
\d\s\w | 1 a | 1ab |
| \S | Not Whitespace.
Matches any character that is not a whitespace character (space, tab, line breaks). |
\w\w\w\w\S\d | Test#1 | test 1 |
| \b | Word boundaries.
Can be used to match a complete word. Word boundaries are the boundaries between a word and a non-word character. |
\bis\b | is; | This
island: |
| {} | The curly braces {…}.
It tells the computer to repeat the preceding character (or set of characters) for as many times as the value inside this bracket. {min,} means the preceding character is matches min times or more. {min,max} means that the preceding character is repeated at least min and at most max times. |
abc{2} |
abcc |
abc |
| .* | Matches any character (except for line terminators), matchs between zero and unlimited times. | .* |
abbb Empty string |
|
| .+ | Matches any character (except for line terminators), matches between one and unlimited times. | .+ | a
abbcc |
Empty string |
| ^ | Anchor ^.The start of the line.
Matches position just before the first character of the string. |
^The\s\w+ | The contest | One contest |
| $ | Anchor $. The end of the line.
Matches position just after the last character of the string. |
\d{4}\sACSL$ | 2020 ACSL | 2020 STAR |
| \ | Escape a special character.
If you want to use any of the metacharacters as a literal in a regex, you need to escape them with a backslash, like: \. \* \+ \[ etc. |
\w\w\w\. | cat. | lion |
| () | Groups.
Regular expressions allow us to not just match text but also to extract information for further processing. This is done by defining groups of characthers and capturing them using the parentheses (). |
^(file.+)\.docx$ | file_graphs.docx
file_lisp.docx |
data.docx |
| \number | Backreference.
A set of different symbols of a regular expression can be grouped together to act as a single unit and behave as a block. \n means that the group enclosed within the n-th bracket will be repeated at current position. |
|||
| \1 | Contents of Group 1. | r(\w)g\1x | regex
Group \1 is e |
regxx |
| \2 | Contents of Group 2. | (\d\d)\+(\d\d)=\2\+\1 | 20+21=21+20
Group \1 is 20 Group \2 is 21 |
20+21=20+21 |
Sample Problems
Typical problems in the category will include: translate an FSA to a Regular Expression; simplify a Regular Expression; determine which Regular Expressions or FSAs are equivalent; and determine which strings are accepted by either an FSA or a Regular Expression.
Problem 1
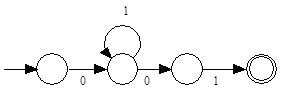
Find a simplified Regular Expression for the following FSA:
Solution:
The expression 01*01 is read directly from the FSA. It is in its most simplified form.
Problem 2
Which of the following strings are accepted by the following Regular Expression "00*1*1U11*0*0" ?
- A. 0000001111111
- B. 1010101010
- C. 1111111
- D. 0110
- E. 10
Solution:
This Regular Expression parses strings described by the union of 00*1*1 and 11*0*0. The RE 00*1*1 matches strings starting with one or more 0s followed by one or more 1s: 01, 001, 0001111, and so on. The RE 11*0*0 matches strings with one or more 1s followed by one or more 0s: 10, 1110, 1111100, and so on. In other words, strings of the form: 0s followed by some 1s; or 1s followed by some 0s. Choice A and E following this pattern.
Problem 3
Which of the following strings match the regular expression pattern "[A-D]*[a-d]*[0-9]" ?
- 1. ABCD8
- 2. abcd5
- 3. ABcd9
- 4. AbCd7
- 5. X
- 6. abCD7
- 7. DCCBBBaaaa5
Solution:
The pattern describes strings the start with zero or more uppercase letters A, B, C, or D (in any order), followed by zero or more lowercase letter a, b, c, or d (in any order), followed by a single digit. The strings that are represented by this pattern are 1, 2, 3, and 7.
Problem 4
Which of the following strings match the regular expression pattern "Hi?g+h+[^a-ceiou]" ?
- 1. Highb
- 2. HiiighS
- 3. HigghhhC
- 4. Hih
- 5. Hghe
- 6. Highd
- 7. HgggggghX
Solution:
The ? indicates 0 or 1 "i"s. The + indicates 1 or more "g"s followed by 1 or more "h"s. The ^ indicates that the last character cannot be lower-case a, b, c, e, i, o, or u. The strings that are represented by this pattern are 3, 6, and 7.
Problem 5
Which of the following strings match the regular expression pattern "^w{3}\.([a-z0-9]([-a-z0-9]{0,61}[a-z0-9])+\.)+[a-z0-9][-a-z0-9]{0,61}[a-z0-9]" ?
- 1. www.google.com
- 2. www.-petsmart.com
- 3. www.edu-.ro
- 4. www.google.co.in
- 5. www.examples.c.net
- 6. www.edu.training.computer-science.org
- 7. www.everglades_holidaypark.com
Solution: This Regular Expression matches a domain name used to access web sites.
RE starts with the subdomain www, continues with a number of names of domains, separated by a dot (Top-level domain (TLD), Second-level domain (SLD), Third-level domain, and so on).
The name of a domain contains only small letters, digits and hyphen. The name can’t begin and can’t finish with a hyphen character. The length of the domain’s name is minimum 2 and maximum 63 characters.
^: the string starts with www;
[a-z0-9] : the first and the last character of the domain's name can be only a small letter or a digit;
[-a-z0-9]{0,61}: the next characters can be small letters, digits or a hyphen character. Maximum 61 characters;
The last sequence [a-z0-9][-a-z0-9]{0,61}[a-z0-9] is for the Top-Level domain, which is not followed by a dot.
The strings that are represented by this pattern are 1, 4 and 6.
Video Resources
Nice two-part video showing the relationship between FSAs and REs.
| 1 - Convert Regular Expression to Finite-State Automaton (Barry Brown) | |
| 2 - Convert Regular Expression to Finite-State Automaton (Barry Brown)
This video uses the symbol "+" to mean "1 or more matches of the previous term". For example, "ab+" is the same as "abb*". In terms of the Kleene Star, zz* = z*z = z+. |
| ACSL Test Prep - Finite State Automaton & Regular Expressions Explained (Mrs. Gupta)
A talked-over presentation discussing the finite state automatons and regular expressions as needed for the American Computer Science League and its tests. |