Data Structures
At the heart of virtually every computer program are its algorithms and its data structures. It is hard to separate these two items, for data structures are meaningless without algorithms to create and manipulate them, and algorithms are usually trivial unless there are data structures on which to operate. The bigger the data sets, the more important data structures are in various algorithms.
This category concentrates on four of the most basic structures: stacks, queues, binary search trees, and priority queues. Questions will cover these data structures and implicit algorithms, not specific to implementation language details. A stack is usually used to save information that will need to be processed later. Items are processed in a “last-in, first-out” (LIFO) order. A queue is usually used to process items in the order in which requests are generated; a new item is not processed until all items currently on the queue are processed. This is also known as “first-in, first-out” (FIFO) order. A binary search tree is used when one is storing a set of items and needs to be able to efficiently process the operations of insertion, deletion, and query (i.e. find out if a particular item is part of the set and if not, which item in the set is close to the item in question). A priority queue' is used like a binary search tree, except one cannot delete an arbitrary item, nor can one make an arbitrary query. One can only find out or delete the smallest element of the set.
Stacks and Queues
A stack supports two operations: PUSH and POP. A command of the form “PUSH(A)” puts the key A at the top of the stack; the command “POP(X)” removes the top item from the stack and stores its value into variable X. If the stack was empty (because nothing had ever been pushed on it, or if all elements have been popped off of it), then X is given the special value of NIL. An analogy to this is a stack of books on a desk: a new book is placed on the top of the stack (pushed) and a book is removed from the top also (popped). Some textbooks call this data structure a “push-down stack” or a “LIFO stack”.
Queues operate just like stacks, except items are removed from the bottom instead of the top. A good physical analogy of this is the way a train conductor or newspaper boy uses a coin machine to give change: new coins are added to the tops of the piles, and change is given from the bottom of each. Some textbooks refer to this data structure as a “FIFO stack”.
Consider the following sequence of 14 operations:
- PUSH(A), PUSH(M), PUSH(E), POP(X), PUSH(R), POP(X), PUSH(I),
- POP(X), POP(X), POP(X), POP(X), PUSH(C), PUSH(A), PUSH(N)
If these operations are applied to a stack, then the values of the pops are: E, R, I, M, A and NIL. After all of the operations, there are three items still on the stack: the N is at the top (it will be the next to be popped, if nothing else is pushed before the pop command), and C is at the bottom. If, instead of using a stack we used a queue, then the values popped would be: A, M, E, R, I and NIL. There would be three items still on the queue: N at the top and C on the bottom. Since items are removed from the bottom of a queue, C would be the next item to be popped regardless of any additional pushes. Sometimes the top and bottom of a queue are referred to as the rear and the front respectively. Therefore, items are pushed/enqueued at the rear of the queue and popped/dequeued at the front of the queue. There is a similarity to the Britsh “queueing up”.
Trees
Trees, in general, use the following terminology: the root is the top node in the tree; children are the nodes that are immediately below a parent node; leaves are the bottom-most nodes on every branch of the tree; and siblings are nodes that have the same immediate parent.
A binary search tree is composed of nodes having three parts: information (or a key), a pointer to a left child, and a pointer to a right child. It has the property that the key at every node is always greater than or equal to the key of its left child, and less than the key of its right child.
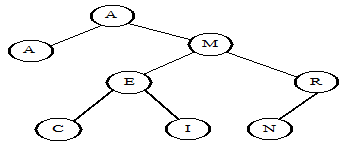
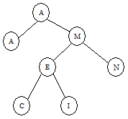
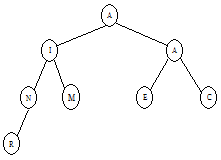
The following tree is built from the keys A, M, E, R, I, C, A, N in that order:
The root of the resulting tree is the node containing the key A; note that duplicate keys are inserted into the tree as if they were less than their equal key. The tree has a depth (sometimes called height) of 3 because the deepest node is 3 nodes below the root. The root node has a depth of 0. Nodes with no children are called leaf nodes; there are four of them in the tree: A, C, I and N. An external node is the name given to a place where a new node could be attached to the tree. In the final tree above, there are 9 external nodes; these are not drawn. The tree has an internal path length of 15 which is the sum of the depths of all nodes. It has an external path length of 31 which is the sum of the depths of all external nodes. To insert the N (the last key inserted), 3 comparisons were needed against the root A (>), the M (>), and the R (≤).
To perform an inorder traversal of the tree, recursively traverse the tree by first visiting the left child, then the root, then the right child. In the tree above, the nodes are visited in the following order: A, A, C, E, I, M, N, and R. A preorder travel (root, left, right) visits in the following order: A, A, M, E, C, I, R, and N. A postorder traversal (left, right, root) is: A, C, I, E, N, R, M, A. Inorder traversals are typically used to list the contents of the tree in sorted order.
Binary search trees can support the operations insert, delete, and search. Moreover, it handles the operations efficiently; in a tree with 1 million items, one can search for a particular value in about log2 1000000 ≈ 20 steps. Items can be inserted or deleted in about as many steps, too. However, binary search trees can become unbalanced, if the keys being inserted are not pretty random. For example, consider the binary search tree resulting from inserting the keys A, E, I, O, U, Y. Sophisticated techniques are available to maintain balanced trees. Binary search trees are “dynamic” data structures that can support an unlimited number of operations in any order.
To search for a node in a binary tree, the following algorithm (in pseudo-code) is used:
- p = root
- found = FALSE
- while (p ≠ NIL) and (not found)
- if (x<p’s key)
- p = p’s left child
- else if (x>p’s key)
- p = p’s right child
- else
- found = TRUE
- end if
- if (x<p’s key)
- end while
Deleting from a binary search tree is a bit more complicated. The algorithm we’ll use is as follows:
- p = node to delete
- f = father of p
- if (p has no children)
- delete p
- else if (p has one child)
- make p’s child become f’s child
- delete p
- else if (p has two children)
- l = p’s left child (it might also have children)
- r = p’s right child (it might also have children)
- make l become f’s child instead of p
- stick r onto the l tree
- delete p
- end if
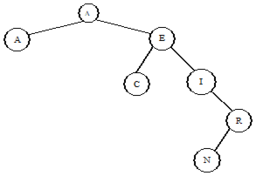
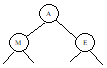
These diagrams illustrate the algorithm using the tree above. At the left, we delete I (0 children); in the middle, we delete the R (1 child); and at the right, we delete the M (2 children).
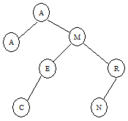
|
|
|
There are also general trees that use the same terminology, but they have 0 or more subnodes which can be accessed with an array or linked list of pointers. Pre-order and post-order traversals are possible with these trees, but the other algorithms do not work in the same way. Applications of general trees include game theory, organizational charts, family trees, etc.
Balanced trees minimize searching time when every leaf node has a depth of within 1 of every other leaf node. Complete trees are filled in at every level and are always balanced. Strictly binary trees ensure that every node has either 0 or 2 subnodes. You may want to consider how there are exactly 5 strictly binary trees with 7 nodes.
Priority Queues
A priority queue is quite similar to a binary search tree, but one can only delete the smallest item and “search” for the smallest. These operations can be done in a guaranteed time proportional to the log of the number of items. One popular way to implement a priority queue is using a heap data structure. A heap uses a binary tree (that is, a tree with two children) and maintains the following two properties: every node is smaller than its two children (nothing is said about the relative magnitude of the two children), and the resulting tree contains no “holes”. That is, all levels of the tree are completely filled, except the bottom level, which is filled in from the left to the right. You may want to stop for a moment to think about how you might make an efficient implementation of a priority queue. This is called a “min-heap”. “Max-heaps” are also possible.
The algorithm for insertion is not too difficult: put the new node at the bottom of the tree and then go up the tree, making exchanges with its parent, until the tree is valid. Consider inserting C into the following heap that has been built by inserting A, M, E, R, I, C, A, N:
The smallest value is always the root. To delete it (and one can only delete the smallest value), one replaces it with the bottom-most and right-most element, and then walks down the tree making exchanges with the child in order to insure that the tree is valid. The following pseudo-code formalizes this notion:
- b = bottom-most and right-most element
- p = root of tree
- p’s key = b’s key
- delete b
- while (p is larger than either child)
- exchange p with smaller child
- p = smaller child
- end while
The following sequence of steps illustrates the building of a heap from the characters A, M, E, R, I, C, A, N:
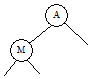 |
 |
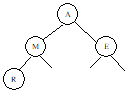
| |
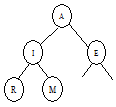 |
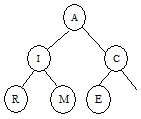 |
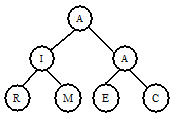 |
|
Sample Problems
Sample Problem 1
Consider an initially empty stack. What is the value of Z when these operations are performed: PUSH(3); PUSH(6); PUSH(8); POP(Y); POP(X); PUSH(X-Y); PUSH(4); PUSH(7); POP(Y); POP(X); PUSH(X-Y); POP(X); POP(Y); PUSH(X*Y);POP(Y); POP(X); PUSH(X/Y); POP(Z)
Solution: The stack will look like the following: 3 6 8 → 3 -2 → 3 -2 4 7 → 3 -2 -3 → 3 6 → 0.5 Therefore, the answer is 0.5 or ½. This sequence illustrates a method for evaluating a postfix expression.
Sample Problem 2
Consider creating a min-heap with the letters in the word PROGRAMMING. What would the bottom-most nodes from left to right be when the entire tree is a heap.
Solution: The final result of the heap has a root A, row 1 is G, G, row 2 is M, I, P, M, and the bottom row is R, O, R, N on the left side of the tree.
Sample Problem 3
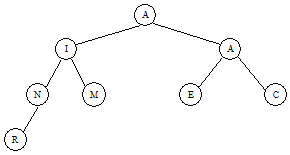
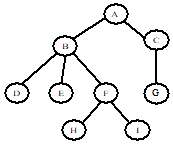
If one traversed this general tree in preorder (visit the root, and then each of the subtrees from left to right), in what order would nodes be visited?
Solution: A is the root node. Then do each of its subtrees using recursion so B has 3 subtrees, F has 2 subtrees, and finally C has 1 subtree. Therefore, the answer is: A B D E F H I C G.
Sample Problem 4
Create a binary search tree from the letters in the word PROGRAMMING. What is the internal path length?
Solution: When drawing the tree, P has a depth of 0, O and R have a depth of 1, G and R have a depth of 2, A and M have a depth of 3, M and N have a depth of 4, I has a depth of 5, and G has a depth of 6. Therefore, the internal path length is 31.
Video Resources
ACSL Videos
The following YouTube videos show ACSL students and advisors working out some ACSL problems that have appeared in previous contests. Some of the videos contain ads; ACSL is not responsible for the ads and does not receive compensation in any form for those ads.
| Data Structures (Stacks and Queues) (Tangerine Code)
A general tutorial on stacks and queues. | |
| Binary Search Tree ACSL Problem (Internal Path Length) (Tangerine Code)
A general tutorial on internal path length of a binary search tree |
Other Videos
There is no shortage of instructional video material covering basic data structures. Here is a series that combine teaching concepts with showing Java code that implements the concepts.
| Data Structures: Linked Lists (HackerRank)
Learn the basics of trees, data structures. This video is a part of HackerRank's Cracking The Coding Interview Tutorial with Gayle Laakmann McDowell. The first half of the video is an clear and eloquent description of binary search trees; the second half walks through very clean Java code that implements the fundamental methods. | |
| Data Structures: Trees (HackerRank)
Learn the basics of trees, data structures. This video is a part of HackerRank's Cracking The Coding Interview Tutorial with Gayle Laakmann McDowell. The first half of the video is an clear and eloquent description of binary search trees; the second half walks through very clean Java code that implements the fundamental methods. | |
| Data Structures: Heaps (HackerRank)
Learn about heaps. This video is a part of HackerRank's Cracking The Coding Interview Tutorial with Gayle Laakmann McDowell. The first half of the video is an clear and eloquent description of binary search trees; the second half walks through very clean Java code that implements the fundamental methods. |